Floating point arithmetic is a popularly esoteric subject in computer science. It is safe to say that every software engineer has heard of floating point numbers. Many have even used them at some point. Few would claim to actually understand them to a reasonable extent and significantly fewer would claim to know all of the corner cases. That last category of engineer is probably mythical or, at best, optimistic. I have dealt with floating-point related issues in the GNU C Library in the past, but I won't claim to be an expert at it. I definitely did not expect to learn about the existence of a new kind of number, as I did a couple of months ago.
This article describes new types of floating point numbers that correspond to nothing in the physical world. The numbers, which I dub pseudo-normal numbers, can create hard-to-track problems for programmers and have even made it into the dreaded Common Vulnerabilities and Exposures (CVE) list.
A brief background: IEEE-754 doubles
Practically every programming language implements 64-bit double floating point numbers using the IEEE-754 double floating point format. The format specifies a 64-bit storage that has one sign bit, 11 exponent bits, and 52 significand bits. Every bit pattern belongs to exactly one of these types of floating point numbers:
- A normal number: The exponent has at least one bit (but not all bits) set. The significand and sign bits may have any value.
- A denormal number: The exponent has all bits clear. The significand and sign bits may have any value.
- Infinity: The exponent has all bits set. The significand has all bits clear and the sign bit may have any value.
- Not a Number (NaN): The exponent has all bits set. The significand has at least one bit set and the sign bit may have any value.
- Zero: The exponent and significand both have all bits clear. The sign bit may have any value, giving rise to that much-loved concept of signed zeroes.
The significand bits describe only the fractional part; the integer is implicitly zero for denormal numbers and zeroes and one for all other numbers. Programming languages map concepts perfectly to these categories of numbers. There is no double floating point number for which at least its classification is unspecified. Due to the wide adoption, one may assume largely consistent behavior across hardware platforms and runtime environments.
If only we could say the same about the larger sibling of the double type: the long double type. The IEEE-754 extended precision format exists, but it does not specify encodings, nor is it a standard across all architectures. We are not here to lament that state of affairs, though; we're investigating the new kind of numbers. We find them in the Intel double extended-precision floating point format.
The Intel double extended-precision floating point format
Section 4.2 in the Intel 64 and IA-32 architectures software developers manual defines the double extended-precision floating point format as an 80-bit value with the layout shown in Figure 1.
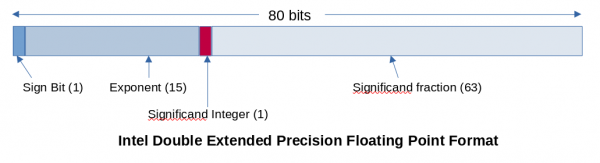
With this definition, our trusty number classifications that we rely on map to the long-double format as follows:
- A normal number: The exponent has at least one bit (but not all bits) set. The significand and sign bits may have any value. The integer bit is set.
- A denormal number: The exponent has all bits clear. The significand and sign bits may have any value. The integer bit is clear.
- Infinity: The exponent has all bits set. The significand has all bits clear and the sign bit may have any value. The integer bit is set.
- Not a Number (NaN): The exponent has all bits set. The significand has at least one bit set and the sign bit may have any value. The integer bit is set.
- Zero: The exponent and significand both have all bits clear. The sign bit may have any value. The integer bit is clear.
Identity crisis
The careful observer might ask two very reasonable questions:
- What if a normal number, infinity, or NaN has its integer bit clear?
- What if the denormal number has its integer bit set?
And with those questions, you will have discovered the new set of numbers. Congratulations!
Section 8.2.2 Unsupported double extended-precision floating-point encodings and pseudo-denormals in the Intel 64 and IA-32 architectures developers manual describes these numbers, so they're not unknown. In summary, the Intel floating point unit (FPU) will generate an invalid operation exception if it encounters a pseudo-NaN (that is, a NaN with integer bit clear), a pseudo-infinity (infinity with integer bit clear), or an unnormal (normal number with integer bit clear). The FPU continues to support pseudo-denormals (denormals with the integer bit set) in the same way it does regular denormals, by generating a denormal operand exception. This has been true since the 387 FPU.
Pseudo-denormal numbers are less interesting because they are treated the same as denormals. The rest though, are unsupported; the manual states that the FPU will never generate these numbers and does not bother giving them a collective name. We need to refer to them collectively in this article, however, so I call them pseudo-normal numbers.
How does one classify pseudo-normal numbers?
As is evident by now, these numbers expose a gap in our worldview of floating point numbers in our programming environment. Is a pseudo-NaN also NaN? Is a pseudo-infinity also infinity? What about unnormal numbers? Should they collectively be their own class of numbers? Should each be its own class of numbers? Why didn't I retire before the third question?
Modifying programming environments to introduce a new class of numbers is not a worthwhile exercise for a single architecture, so that is out of the question. Shoehorning these numbers into existing classes could be based on which class they are pseudos of. Alternatively, we could collectively consider them NaNs (specifically, signaling NaNs) because like signaling NaNs, operating on them generates an invalid operation exception.
Undefined behavior?
A valid question here is whether we should care at all. The C standard, for example, in section 6.2.6 Representations of types, states that "Certain object representations need not represent a value of the object type," which fits our situation. The FPU will never generate these representations for the long double type, so one could argue that passing these representations in a long double is undefined. That is one way to answer the question about classification, but it essentially punts understanding the hardware specification to the user. It implies that every time a user reads a long double from a binary file or the network, they need to validate that the representation is valid according to the underlying architecture. This is something that the fpclassify function and friends ought to do, but sadly they do not.
If many answers are possible, many answers you'll get
To recognize whether an input is NaN, the GNU Compiler Collection (GCC) passes on the answer the CPU gave it. That is, it implements __builtin_isnanl by performing a floating point comparison with the input. When an exception is generated (as it does with a NaN), the parity flag is set, which indicates an unordered result, thus indicating that the input is NaN. When the input is any of the pseudo-normal numbers, it generates an invalid operation exception, so all of these numbers are categorized as NaN.
The GNU C Library (glibc), on the other hand, looks at the bit pattern of the number to decide its classification. The library evaluates all of the bits of the number to decide whether the number is NaN in __isnanl or __fpclassify. During this evaluation, the implementation assumes that the FPU will never generate the pseudo-normal numbers and ignores the integer bit. As a result, when the input is any of the pseudo-normal numbers (except pseudo-NaNs, of course), the implementation "fixes" the numbers to their non-pseudo counterparts and makes them valid!
Mostly (but not completely) harmless
The glibc implementation of isnanl assumes that it always gets a correctly formatted long double. That is not an unreasonable assumption, but it puts the onus on each programmer to validate binary long double data read from files or the network before passing it on to isnanl, which, ironically, is a validating function.
These assumptions led to CVE-2020-10029 and CVE-2020-29573. In both of these CVEs, functions (trigonometric functions in the former and the printf family of functions in the latter) rely on valid inputs and end up with potentially exploitable stack overflows. We fixed CVE-2020-10029 by considering pseudo-normal numbers as NaN. The functions would check the integer bit and bail out if it was clear.
The fix history of CVE-2020-29573 is a bit more interesting. Some years ago, as a cleanup, glibc replaced the use of isnanf, isnan, and isnanl with the standard C99 macro isnan, which expands to the appropriate function based on input. Subsequently, another patch went in to optimize the isnan C99 macro definition so that it uses __builtin_isnan when it is safe to do so. This inadvertently fixed CVE-2020-29573, because the check for validity now started failing for pseudo-normal numbers.
Agreeing on the answer
The CVEs prompted us (the GNU toolchain community) to talk more seriously about the classification of these numbers with respect to the C library interface. We discussed this in the glibc and GCC communities and agreed that these numbers should be considered signaling NaNs in the context of the C library interfaces. It does not mean, however, that libm will strive to treat these numbers consistently as NaNs internally or provide exhaustive coverage. The intent is not to define behavior for these numbers; it is only to make classification consistent across the toolchain. More importantly, we agreed on guidelines in cases where misclassification of these numbers results in crashes or security issues.
That, friends, was a story of the unnormal, the pseudo-NaN, and the pseudo-infinity. I hope you never run into those, but if you do, hopefully we've made it easier for you to deal with them.
Last updated: February 5, 2024