Hash tables are an important part of dynamic programming languages. They are widely used because of their flexibility, and their performance is important for the overall performance of numerous programs. Ruby is not an exception. In brief, Ruby hash tables provide the following API:
- insert an element with given key if it is not yet on the table or update the element value if it is on the table
- delete an element with given key from the table
- get the value of an element with given key if it is in the table
- the shift operation (remove the earliest element inserted into the table)
- traverse elements in their inclusion order, call a given function and depending on its return value, stop traversing or delete the current element and continue traversing
- get the first N or all keys or values of elements in the table as an array
- copy the table
- clear the table
Since Ruby 1.9, traversing hash tables and shift operation should be done in the order elements were included. In other words, elements included earlier should be traversed first. The current implementation of Ruby hash tables is based on an old package written by Peter Moore, with modern murmurhash and siphash algorithms used for hashing Ruby values.
Moore's original implementation has been changed a lot and the current Ruby hash tables have the following organization:
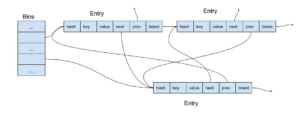
The typical Ruby hash table (very small hash tables have a different organization) has an array of bins, each bin containing a pointer to a list of table elements (entries, in the Ruby hash table terminology). The calculated hash is translated into the table bin by a modulo operation, which is actually a mask operation as the bin array is of the size of a power of 2.
As you can see, entries have 3 pointers: two for a doubly linked list of entries in their order of inclusion and one for a list of entries corresponding the same bin (in other words, for colliding entries). Using a single linked list for collisions saves memory but makes deleting arbitrary entries during traversal, not a trivial task. So the actual Ruby hash table API is even more complicated than what I described.
When a Ruby hash table's load factor becomes too big, a new, larger bin array is created.
Modern processors have several levels of cache. Usually, the CPU reads one or a few lines of the cache from memory (or another level of cache). So CPU is much faster at reading data stored close to each other. The current implementation of Ruby hash tables does not fit well with modern processor cache organization, which requires better data locality for faster program speed.
So, how can we improve data locality?
First, we can remove the collision lists by switching to an open addressing hash table where each bin corresponds at most to one entry. Although open addressing needs more bins than the original separate chaining hash tables, we can afford this as we remove one pointer by switching to open addressing. As a result of this switch, we improve data locality for processing entries by their key.
The tendency has been to move from chaining hash tables to open addressing hash tables due to their better fit to modern CPU memory organizations. CPython recently made this switch. GCC has widely-used such hash tables internally for more than 15 years.
To improve data locality for processing entries by their inclusion order, we can remove the doubly linked list and put the entries into an array. It also removes two pointers, and the new entry becomes exactly two times smaller than the original one. That also decreases entry footprint and increases data locality. Removing the lists lets us avoid pointer chasing, a common problem that produces bad data locality.
So our proposed Ruby hash table has the following organization:
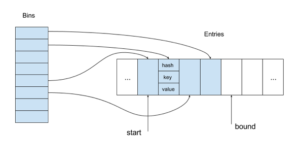
The entry array contains table entries in the same order as they were inserted. When the first entry is deleted, a variable containing the index of the current first entry (start) is incremented. In all other cases of deletion, we just mark the entry as deleted by using a reserved hash value.
Bins provide access to entries by their keys. The key hash is mapped to a bin containing the index of the corresponding entry in the entry array (using an index instead of a pointer can be memory saving when we use 8-, 16- or 32-bit indices for reasonable size tables on 64-bit machines).
The size of the array bin is always a power of two, which it makes mapping very fast by using the corresponding lower bits of the hash. Generally, it is not a good idea to ignore some part of the hash. But the alternative approach is worse. For example, we could use a modulo operation for mapping and a prime number for the size of bin array. Unfortunately, the modulo operation for large 64-bit numbers is extremely slow (it takes more 100 cycles on modern Intel CPUs).
Still, the remaining bits of the hash value can be used when the mapping results in a collision. That is also an improvement in comparison with the original tables. We use a secondary hash value function analogous to one in the new CPython hash table implementation. The secondary hash value function is a function of the collision bin index and original hash value. This choice of function guarantees that we can traverse all bins and finally find the corresponding bin, as after several iterations the function becomes X_next = (5 * X_prev + 1) mod pow_of_2, which is a full cycle linear congruential generator since it satisfies the requirements of the Hull-Dobell theorem. By the way, I suspect that the function lookdict in CPython might cycle in extremely rare cases, as X_prev in the function can be more than the size of the table.
When an entry is removed from the table, besides marking the slot as deleted using a special hash value, we also mark the bin by a special value in order to find entries, which had a collision with the removed entries.
There are two reserved values for bins. One denotes an empty bin, while the other one denotes a bin containing a deleted entry.
The length of the bin array is always twice the entry array length. This maintains a healthy table load factor. To improve table memory footprint, we use 8, 16, 32-bits indices on a 64-bit system for smaller tables. As bins are a smaller part of the all table footprint for small tables, we could even increase the bin array two times to decrease the load factor and the collision number even more. But currently, this approach is not used.
The trigger of rebuilding the table is always the case when we cannot insert an entry at the end of the entry array. As opposed to the original hash tables, new arrays can be smaller after rebuilding. This can happen when we remove a lot of entries.
Table rebuilding is done by creating new array entries and bins of appropriate size. We could try to reuse the arrays in some cases by moving non-deleted entries to the start of the array. But this makes little sense, as the most expensive part is entry moves and such an approach just complicates the implementation.
Analysis of the hash table usage in Ruby on Rails shows that the majority of hash tables are small. We prevent allocations of bins and use a linear search for very small tables less than 5 entries. It saves memory and makes an access to the entries by keys faster for such small tables by saving time to maintain and work with data in the bins.
The original Ruby hash tables use the same approach for tables of less than 7 entries but the implementation is more complicated as it needs a different table representation.
Here is the performance comparison of original and proposed hash tables on 27 MRI hash table benchmarks. We use two major targets for this: x86-64 and ARM.
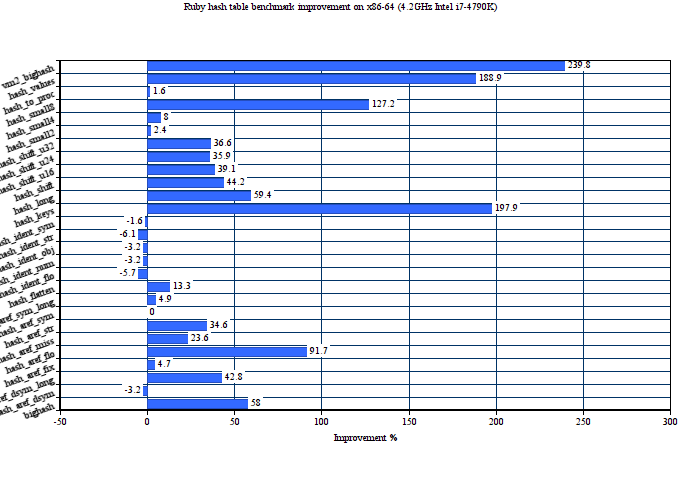
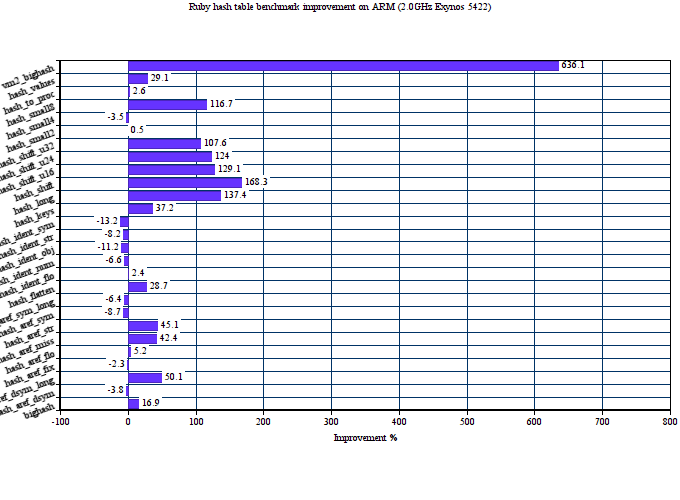
The average performance improvement on Intel Haswell for the proposed hash tables is about 46%. On ARM, it is even bigger 59%. The proposed implementation also consumes less memory in average than the old one. The below graph shows memory consumption in bytes on x86-64 depending on the number of entries in the hash table.
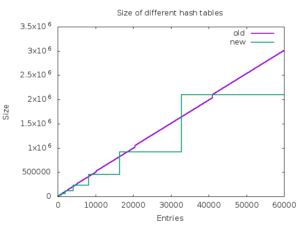
The proposed implementation is also more straightforward. It permits to simplify the Ruby hash table API in future by avoiding of the original hash tables' problems with deleting entries during traversal.
Although the new design seems simple, achieving acceptable results required a lot of testing of different variants of the implementation. That is how performance work is usually done.
As an example of such work, one variant of the new hash table implementation had a faster solution to solve the problem of possible denial attacks based on hash collisions:
- When a new table entry was inserted, we just counted collisions with entries with the same hash (more accurately a part of the hash) but different keys and when some threshold was achieved, we rebuilt the table and started to use a crypto-level hash function. In reality, the crypto-level function would be never used until someone really tries to do the denial attack.
- Such approach permitted to use faster non-crypto level hash functions in the majority of cases. It also would permit easily to switch to the usage of other slower crypto-level functions (without losing speed in real world scenario), e.g. sha-2 or sha-3. The cryptographic function siphash currently used in MRI is pretty a new function and it is not time-tested yet as older functions.
Although it is not documented, Ruby function hash should be the same as hash function used inside the hash tables and its value should be always the same for an object during one MRI run. Therefore, this approach did not survive the final variant of the hash tables.
It took 8 months from submitting the initial code to committing it into MRI repository (please see issue 12142). Now the new hash table implementation is a part of MRI 2.4.
The hash table implementation discussion contains more 170 posts. Reading the posts can be quite educative and can be a good case of studying open source development aspects and issues.
On a side note, I'd like to thank my managers for permission to invest part of my time to work on Ruby performance in addition to my major responsibilities.
Last updated: June 7, 2023
